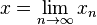Eksponen

Eksponen adalah perkalian yang diulang-ulang. Orang menulis eksponen dengan indeks di atas, yang akan terlihat sebagai berikut:

x y

. Terkadang hal itu tak mungkin. Kemudian orang menulis eksponen menggunakan tanda ^: 2^3 berarti

23

.
Bilangan

x

disebut bilangan pokok, dan bilangan

y

disebut eksponen. Sebagai contoh, pada

23

, 2 adalah bilangan pokok dan 3 eksponen.
Untuk menghitung

23

seseorang harus mengalikan 3 kali terhadap angka 2. Sehingga $2^3=2 \cdot 2 \cdot 2$ . Hasilnya adalah $2 \cdot 2 \cdot 2=8$ . Apa yang dikatakan persamaan bisa juga dikatakan dengan cara ini: 2 pangkat 3 sama dengan 8.
Contoh:

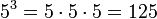
$5^3=5\cdot{} 5\cdot{} 5=125$
$x^2=x\cdot{} x$
$1 x = 1$ untuk setiap bilangan x

Jika eksponen sama dengan 2, maka disebut persegi karena area persegi dihitung menggunakan

a 2

. Sehingga

x 2

adalah persegi dari

x

Jika eksponen sama dengan 3, maka disebut kubik karena volume kubus dihitung dengan

a 3

. Sehingga

x 3

adalah kubik

x

Jika eksponen sama dengan -1 orang harus menghitung inversi bilangan pokok. Sehingga: $x^{-1}=\frac{1}{x}$ Jika eksponen adalah integral dan kurang dari 0, orang harus membalik bilangan dan menghitung pangkat. Sebagai contoh:

$2^{-3}=(\frac{1}{2})^3=\frac{1}{8}$

Jika eksponen sama dengan $\frac{1}{2}$ hasilnya adalah akar persegi bilangan pokok. Sehingga $x^{\frac{1}{2}}=\sqrt{x}.$ Contoh:

$4^{\frac{1}{2}}=\sqrt{4}=2$

Dengan cara yang sama, jika eksponen $\frac{1}{n}$ hasilnya adalah akar ke-n, sehingga:

$a^{\frac{1}{n}}=\sqrt[n]{a}$

Jika eksponen merupakan bilangan rasional $\frac{p}{q}$ , hasilnya adalah akar ke-q bilangan pokok yang dipangkatkan p,
Eksponen bisa juga tak rasional. Untuk menjadikan bilangan pokok a menjadi pangkat ke-x yang tak rasional, kita menggunakan rangkaian ketidakterhinggaan bilangan rasional (x_i), yang limitnya adalah x:

$x=\lim_{n\to\infty}x_n$

seperti ini: $a^x=\lim_{n\to\infty}a^{x_n}$
A. Sifat eksponen

$\left(a\cdot b\right)^n = a^n\cdot{}b^n$
$\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n},\quad b\neq 0$
$a^r \cdot{} a^s = a^{r+s}$
$\frac{a^r}{a^s} = a^{r-s},\quad a\neq 0$
$a^{-n} = \frac{1}{a^n},\quad a\neq 0$
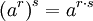
$\left(a^r\right)^s = a^{r\cdot s}$
$a^0 = 1,\quad a\neq 0$ : Bila bilangan pokok lebih besar daripada 1 dan eksponen 0, jawabannya 1. Jika bilangan pokok dan pangkat sama dengan 0, jawabannya tak terdefinisikan.

Ekponen matriks bisa pula dihitung. Matriks itu harus persegi. Sebagai contoh: $I^2=I \cdot I=I$

Persamaan Ekoponen

Adalah persamaan yang didalamnya terdapat pangkat yang berbentuk fungsi dalam x (x sebagai peubah).
[Ket. : Usahakan setiap bilangan pokok ditulis sebagai bilangan berpangkat dengan bilangan dasar 2, 3, 5, 7, dst].
BENTUK-BENTUK
A. a^f(x) = a^g(x) ® f(x) = g(x)

® Samakan bilangan pokoknya sehingga pangkatnya dapat disamakan.
contoh :

2 SUKU ® SUKU DI RUAS KANAN, 1 SUKU DI RUAS KIRI

Ö(8^2x-3) = (32^x+1)^1/4
(2³)^(2x-3)1/2 = (2⁵)^(x+1)1/4
2^(6x-9)/2 = 2^(5x-5)/4
(6x-9)/2 = (5x-5)/4
24x-36 = 10x+10
14x = 46
x = 46/14 = 23/7
3^x²-3x+2 + 3^x²-3x = 10
3².3^{^x²-3x}+3^{^x²-3x} = 10
9. ^{3^x²-3x} + 3^{^x²-3x} = 10
10. 3^x²-3x = 10
3^{x² - 3x} = 3⁰
x² - 3x = 0
x(x-3) = 0
x1 = 0 ; x2 = 3

3 SUKU ® GUNAKAN PEMISALAN

2^{2x + 2} - 2 ^x+2 + 1 = 0
2².2^2x - 2².2^x + 1 = 0
Misalkan : 2^x = p
2^2x = (2x)² = p²
4p² -4p + 1 = 0
(2p-1)² = 0
2p - 1 = 0
p =1/2
2^x = 2^-1
x = -1
B. a^f(x) = b^f(x) ® f(x) = 0

Bilangan pokok berbeda, pangkat sama. Pangkatnya = 0.
Contoh:

3^x²-x-2 = 7^x²-x-2
x² - x -2 = 0
(x-2)(x+1) = 0
x1 = 2 ; x2 = -1

C. a^f(x) = b^f(x) ® f(x) log a = g(x) log b
Bilangan pokok berbeda, pangkat berbeda. Diselesaikan dengan menggunakan logaritma.
Contoh:

4^x-1 = 3^x+1
(x-1)log4 = (x+1)log3
xlog4 - log4 = x log 3 + log 3
x log 4 - x log 3 = log 3 + log 4
x (log4 - log3) = log 12
x log 4/3 = log 12
x log 4/3 = log 12
x = log 12/ log 4/3 = ^4/3 log 12

D. f(x) ^g(x) = f(x) ^h(x)® Bilangan pokok (dalam fungsi) sama, pangkat berbeda.Tinjau beberapa kemungkinan.

Pangkat sama g(x) = h(x)
Bilangan pokok f(x) = 1 ket: 1^g(x) = 1^h(x) = 1
Bilangan pokok f(x) = -1
Dengan syarat, setelah nilai x didapat dari f(x)=-1 , maka nilai
pangkatnya yaitu g(x) dan h(x) kedua-duanya harus genap atau kedua-duanya harus ganjil.

ket :
g(x) dan h(x) Genap : (-1)^g(x) = (-1)^h(x) = 1
g(x) dan h(x) Ganjil : (-1)^g(x) = (-1)^h(x) = -1
Bilangan pokok f(x) = 0
Dengan syarat, setelah nilai x didapat dari f(x) = 0, maka nilai pangkatnya yaitu g(x) dan h(x) kedua-duanya harus positif.

ket : g(x) dan h(x) positif ® 0^g(x) = 0^h(x) = 0

Contoh:

(x² + 5x + 5)^3x-2 = (x² + 5x + 5)^2x+3

Pangkat sama
3x - 2 = 2x + 3 ® x1 = 5
Bilangan pokok = 1
x² + 5x + 5 = 1
x² + 5x + 4 = 0 ® (x-1)(x-4) = 0 ® x2 = 1 ; x3 = 4
Bilangan pokok = -1
x² - 5x + 5 = -1
x² - 5x + 6 = 0 ® (x-2)(x-3) = 0 ® x = 1 ; x = 4

g(2) = 4 ; h(2) = 7 ; x=2 tak memenuhi karena (-1)4 ¹ (-1)7
g(3) = 7 ; h(3) = 9 ; x4 = 3 memenuhi karena (-1)7 = (-1)9 = -1

Logaritma

Logaritma adalah operasi matematika yang merupakan kebalikan dari eksponen atau pemangkatan.
Rumus dasar logaritma:
b^c= a ditulis sebagai ^blog a = c (b disebut basis)
Beberapa orang menuliskan ^blog a = c sebagai log_ba = c

Notasi

Di Indonesia, kebanyakan buku pelajaran Matematika menggunakan notasi ^blog a daripada log_ba. Buku-buku Matematika berbahasa Inggris menggunakan notasi log_ba
Beberapa orang menulis ln a sebagai ganti ^elog a, log a sebagai ganti ¹⁰log a dan ld a sebagai ganti ²log a.
Pada kebanyakan kalkulator, LOG menunjuk kepada logaritma berbasis 10 dan LN menunjuk kepada logaritma berbasis e.
Pada beberapa bahasa pemrograman komputer seperti C,C++,Java dan BASIC, LOG menunjuk kepada logaritma berbasis e.
Terkadang Log x (huruf besar L) menunjuk kepada ¹⁰log x dan log x (huruf kecil L) menunjuk kepada ^elog x

Rumus Logaritma

a^c = b → ª log b = c
r
a = basis
b = bilangan yang dilogaritma
c = hasil logaritma
Sifat-sifat Logaritma
ª log a = 1
ª log 1 = 0
ª log aⁿ = n
ª log bⁿ = n • ª log b
ª log b • c = ª log b + ª log c
ª log ^b/c = ª log b – ª log c
ªˆⁿ log b ^m = ^m/n • ª log b
ª log b = 1 ÷ ^b log a
ª log b • ^b log c • ^c log d = ª log d
ª log b = ^c log b ÷ ^c log a

Persamaan Logaritma
Adalah persamaan yang didalamnya terdapat logaritma dimana numerus ataupun bilangan pokoknya berbentuk suatu fungsi dalam x.

Masalah : Menghilangkan logaritma

^alog f(x) = ^alog g(x) ® f(x) = g(x)
^alog f(x) = b ® f(x) =ab
^f(x)log a = b ® (f(x))^b = a
Dengan syarat x yang didapat dari persamaan tersebut harus terdefinisi. (Bilangan pokok > 0 ¹ 1 dan numerus > 0 )
Contoh:
Tentukan nilai x yang memenuhi persamaan berikut !
^{xlog 1/100 = -1/8

x^-1/8 = 10^-2

(x ^-1/8) ^-8 = (10-2)^-8

x = 10 ¹⁶

^xlog 81 - 2 ^xlog 27 + ^xlog 9 + 1/2 ^xlog 729 = 6

^xlog 3⁴ - 2 ^xlog3³ + ^xlog² + 1/2 ^xlog 3⁶ = 6

4 ^xlog3 - 6 ^xlog3 + 2 ^xlog3 + 3 ^xlog 3 = 6

3 ^xlog 3 = 6

^xlog 3 = 2

x² = 3 ® x = Ö3 (x>0)

^xlog (x+12) - 3 ^xlog4 + 1 = 0

^xlog(x+12) - ^xlog 4³ = -1

^xlog ((x+12)/4³) = -1

(x+12)/4³ = 1/x

x² + 12x - 64 = 0

(x + 16)(x - 4) = 0

x = -16 (TM) ; x = 4

²log²x - 2 ²logx - 3 = 0

misal : ²log x = p

p² - 2p - 3 = 0

(p-3)(p+1) = 0

p₁ = 3

²log x = 3

x₁ = 2³ = 8

p₂ = -1

²log x = -1

x₂ = 2^-1 = 1/2}

Charys's Blog

Translator

Eksponen dan Logaritma

Eksponen